Tutorial:
M O N T E   C A R L O   S I M U L A T I O N

    
Any financial analysis requiring to project future outcomes contains some level of uncertainty. Unless you have a good crystal ball, these projections will seldom turn out to be exactly as forecasted. Monte Carlo simulation is a technique that helps you to model uncertainties behind these projections. The simulation is a sophisticated scenario analysis that can model thousands of scenarios in seconds.

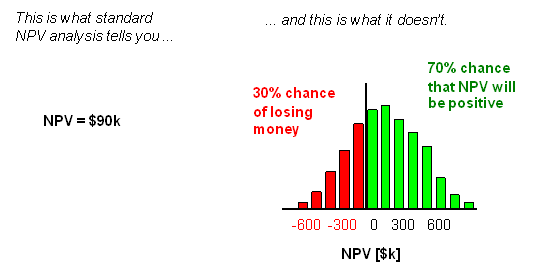
In the case of the ROI analysis with Monte Carlo simulation, for example, rather than providing a single return on investment figure, like the standard net present value (NPV) analysis shown on the left below, the Monte Carlo simulation returns a range of possible outcomes (shown on the right), together with the probability of their occurrences.

In this example, Monte Carlo simulation allows you to determine not just whether an investment will be profitable, but how likely it is to be profitable and how profitable it is likely to be. The chart below reveals that there is a 70% chance that this particular investment will make money. But there is also a 30% chance that it will be a loss. 		 


What standard NPV doesn't tell you

Unlike typical scenario or what-if analyses that allow you to analyze the impact of changing one input variable at a time, Monte Carlo simulation analyzes all possible combinations at once. In a typical scenario analysis, you manually calculate as many scenarios as you deem necessary. Monte Carlo simulation, on the other hand, calculates these scenarios automatically, based on your definition of simulation parameters. It allows you to run thousands of scenarios instead of the few in a typical what-if analysis.

Monte Carlo simulation was popularized by physicists in the 1950s at the dawn of the computer age and it got its name from the Monte Carlo Casino in Monaco. Games of chance played at a casino exhibit random behavior that is bound by the characteristics of the game. When rolling a die for example, you know that a number between 1 and 6 will come up, but you don't know which one.

Similarly, in a capital investment project you may know the range of possible financial outcomes, but you don't know exactly which one will materialize. Monte Carlo simulation allows you to model all potential scenarios driven by the uncertain variables. These scenarios are defined by the probability distributions and simulation parameters.

Probability distributions

There are few probability distributions that are used frequently in the business world. Many times a normal distribution (also known as bell curve) is a good representation of a business situation. The normal distribution is symmetrical around the mean with open tails on both ends (see left chart below).

There may be cases, however, where other distributions may be more appropriate. For example, when modeling days payable outstanding (DPO) in a cash flow analysis, it may be more appropriate to set a fixed range of possible values of DPO and model same likelihood of occurrence across that range. In this case the uniform distribution should be used.

A distribution that is skewed to one side may be appropriate in other cases. Unit sales of new products in a ROI analysis, for example, most likely won't be negative. On the other hand, they may be much higher than the most likely estimates if the product is a hit. Hence, instead of a symmetrical distribution a skewed distribution could be used. The triangular distribution is such a distribution and in this example its minimum could be set at zero to avoid negative unit sales in the simulation.


Normal distributionUniform distributionTriangular distribution


Once the appropriate distribution is selected, its simulation parameters need to be defined. These parameters depend on the type of distribution and are described in more details in FinanceIsland's financial analysis tools.

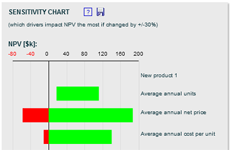
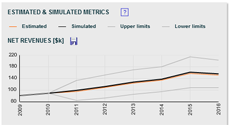
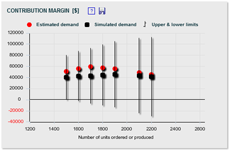
Simulation and results visualization

Monte Carlo simulation uses the selected distributions and their simulation parameters to automatically generate thousands of scenarios (or iterations), usually in just a few seconds. At each iteration, the simulation selects a random value for each identified variable based on the defined parameters and calculates the corresponding outcome.

After all iterations, all iteration outcomes can be visualized, the visualization though depends on the type of analysis. In the ROI analysis for example, the range (or probability distribution) of NPV is depicted. In the cash flow analysis, on the other hand, the simulation outcomes are translated into a range of possible cash flows over time.

If the simulation results are visualized through a probability distribution, the resulting probability distribution may resemble a normal distribution even if other distribution types were selected to model the input variables. This is due to the fact that many real life situations can be described with a normal distribution if the sample size is large enough. Since the Monte Carlo simulation analyzes thousands of scenarios, i.e., thousands of samples, the resulting probability distribution may resemble a normal distribution. This fact is described through a mathematical theorem, known as the central limit theorem.

Although Monte Carlo simulation can be run for all input variables, it is recommended to focus the simulation on the key drivers of the analyzed metric. This can simplify the analysis and helps to better understand the results. The sensitivity chart, which points to the most relevant drivers, can be used to identify these key drivers.

The Monte Carlo simulation used in FinanceIsland's tools assumes that the input variables are relatively independent of each other. If this is not the case or if some inputs are mutually exclusive, a Monte Carlo simulation customized for the specific analysis may be more appropriate to use.

Beware of Black Swans

One aspect to keep in mind when running any scenario analysis, including Monte Carlo simulation, is that the analysis is only accurate for scenarios not wildly different than the most likely estimates. There may be, however, extraordinary, though not absolutely unlikely events where one or more variables are significantly different from the one modeled, which would dramatically impact the results.

In the case of ROI analysis, for example, the number of units sold could be hundred times higher than forecasted if the new product exceeds any possible expectations. Or the product may not sell at all if the economy crashes and customers stop buying these types of products.

Events like these, referred to also as Black Swans, have a low likelihood of occurrence, but big impact. Since Black Swans are unexpected by definition, they are not modeled in financial analyses. These events would also not fit the cost structures and interdependencies used in the financial models.

Bottom line

Although Monte Carlo simulation will not eliminate uncertainties in business decisions, it can help you to understand them in normal business circumstances. For example, if there is a chance of negative financial outcome in your business, Monte Carlo simulation allows you to assess what might go wrong and helps you to be proactive with the decisions you make. Similarly, if you're allocating resources among several projects, Monte Carlo simulation helps you to determine which ones have the greatest chance of success.

Monte Carlo simulation can especially be helpful in financial projections for projects that are not based on repeated past experiences. These projections are most often badly flawed. Monte Carlo simulation will not help to predict all possible events, but it will help to prepare for those events.